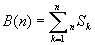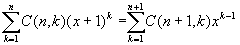僷僗僇儖偺悢嶰妏宍偲偄傠偄傠側悢
搶戝捗崅摍妛峑丂丂怷尨丂懃抝
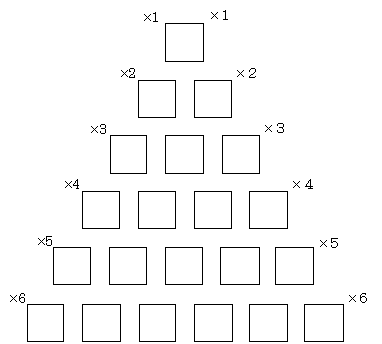
亂侾亃僷僗僇儖偺悢嶰妏宍
嘆嵟忋抜偺彙栚偵偼侾傪擖傟側偝偄丅
嘇墶俀屄偺彙栚偺悢偺榓傪偡偖壓偺抜偺娫偺彙栚偵擖傟側偝偄丅扐偟丄椬偺彙栚偑側偄偲偙傠偼侽偲偟偰寁嶼偟側偝偄丅

僷僗僇儖偺悢嶰妏宍偼丂丂乮侾乯丂嵟抁宱楬偺屄悢丂丂乮俀乯丂(x+y)n偺揥奐乵俀崁掕棟乶丂丂乮俁乯丂慻崌偣偺悢丂丂側偳傪媮傔傞偺偵棙梡偝傟傞丅崅峑偺嫵堢幚慔偱傕傛偔棙梡偝傟偰偄傞偟丄懡偔偺恖偑傛偔抦偭偰偄傞丅偲偙傠偑丄偙傟偐傜弎傋傞偙偲偼偦傫側偵擄偟偄偙偲偱傕側偄偟丄棟桼傕柧傜偐偩偟丄棙梡壙抣傕偁傞偲巚偆偺偵巹偑弌偔傢偟偨彂暔偺拞偵偼慡偔怗傟傜傟偰偼偄側偄丅
亂俀亃僇僞儔儞悢偲僷僗僇儖偺悢嶰妏宍
壓偺彙栚偺拞偵僷僗僇儖偺悢嶰妏宍偺嶌傝曽偲摨條偵偟偰悢傪擖傟側偝偄丅
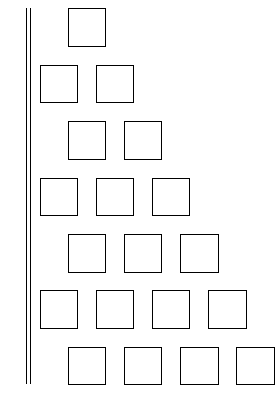
仏暻偺墶偺俀楍偵尰傟傞悢偑乽僇僞儔儞悢乿偲屇偽傟傞悢偱偡丅
仏値妏宍傪岎傢傜側偄懳妏慄偱嶰妏宍暘妱偡傞曽朄偺悢偼壗捠傝偁傞偐丅乮僆僀儔乕偺栤戣乯
仏墘嶼丂a1丒a2丒丒丒an 偵妵屖傪晅偗偰寁嶼偵弴彉傪晅偗偨偄丅壗捠傝偺曽朄偑偁傞偐丅乮僇僞儔儞偺栤戣乯
偙傟傜偺悢偑僇僞儔儞悢偲偄傢傟傞傕偺偱偡丅
亂俁亃僼傿儃僫僢僠悢楍偲僷僗僇儖偺悢嶰妏宍
壓偺彙栚偺拞偵僷僗僇儖偺悢嶰妏宍偺嶌傝曽偲摨條偵偟偰悢傪擖傟側偝偄丅
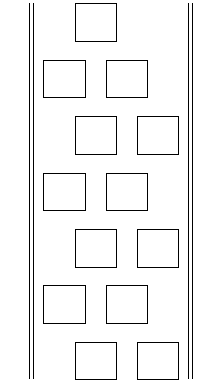
仏偙偙偵尰傟傞悢偑乽僼傿儃僫僢僠悢楍乿偱偡丅
仏慟壔幃丂丂a1亖侾丂,丂a2亖侾丂,丂an+2= an+1+an丂偱掕媊偝傟傞悢楍傪乽僼傿儃僫僢僠悢楍乿偲尵偄傑偡丅
亂係亃戞俀庬僗僞乕儕儞僌悢偲僷僗僇儖偺悢嶰妏宍
壓偺彙栚偺拞偵僷僗僇儖偺悢嶰妏宍偺嶌傝曽偲摨條偵偟偰悢傪擖傟側偝偄丅
偨偩偟丄塃忋偺悢偼塃忋忋抜偺亊i傪巤偟偨屻偵嵍忋偺悢偲偺榓傪媮傔傑偡丅
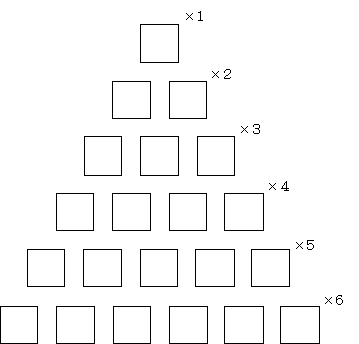
仏偙偙偵尰傟傞悢傪戞俀庬僗僞乕儕儞僌悢値俽倠偲尵偄傑偡丅
仏傑偨丄奺抜偺悢偺榓傪儀儖悢俛乮値乯偲尵偄傑偡丅
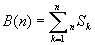
亂俆亃戞侾庬僗僞乕儕儞僌悢偲僷僗僇儖偺悢嶰妏宍
壓偺彙栚偺拞偵僷僗僇儖偺悢嶰妏宍偺嶌傝曽偲摨條偵偟偰悢傪擖傟側偝偄丅
偨偩偟丄塃忋偺悢偼塃抂亊値傪巤偟偨屻偵嵍忋偺悢偲偺榓傪媮傔傑偡丅
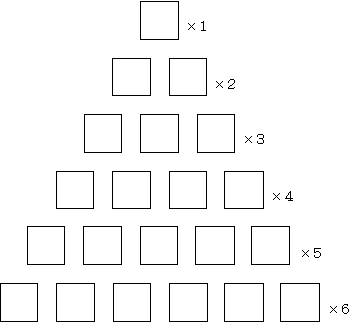
仏偙偙偵弌偰偔傞悢偼戞侾庬僗僞乕儕儞僌悢偲尵傢傟傞悢偺愨懳抣偱偡丅
戞侾庬僗僞乕儕儞僌悢偺愨懳抣傪丂俠乮値丆倠乯丂偲偡傞偲師偺幃偑惉傝棫偪傑偡丅
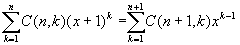
椺偊偽丄値亖俁偺偲偒
俀乮倶亄侾乯亄俁乮倶亄侾乯俀亄乮倶亄侾乯俁亖俇亄侾侾倶亄俇倶俀亄倶俁
仸晄巚媍側嶰妏宍丗忋婰偲帡偨傛偆側榖偑乽榖戣尮悢妛乿偺P1034偵乽晄巚媍側嶰妏宍乿偲偟偰嵹偭偰偄傑偡丅