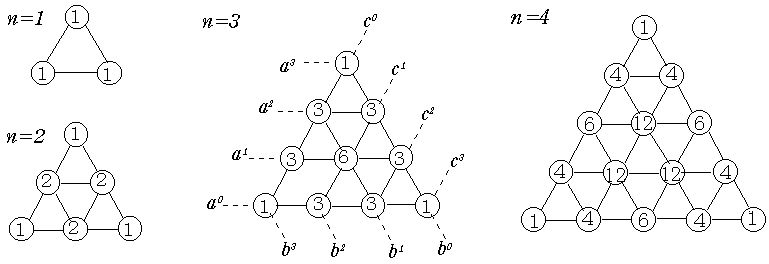
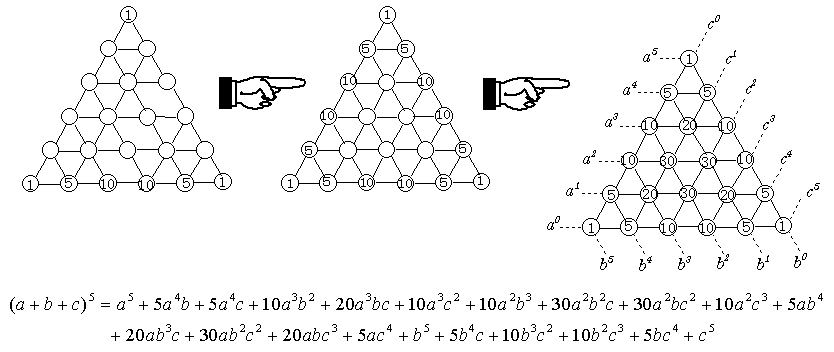丂丂丂傑偨丄慻崌偣傪梡偄偨暿夝偲偟偰丄俋夞偺堏摦偺偆偪丄仾偲側傞堏摦傪偡傞係嬫夋傪慖傋偽摴偡偠偑侾偮寛傑傞偺偱丄俋俠係亖9俠5亖侾俀俇捠傝偲偡傞曽朄傕摨帪偵嵹偣傜傟偰偄傞丅
丂庼嬈拞偵偼丄偙偺俀偮傪埖偆梊掕偱偁偭偨偑丄悢偊忋偘偺曽朄偱夝偄偨惗搆偑偄偰傃偭偔傝偟偨丅惓捈側偲偙傠丄崅峑帪戙偵偁傑傝悢妛偑摼堄偱側偐偭偨巹偼丄帺暘帺恎偼偠傔偰偺懱尡偱偁偭偨偺偱丄乽傆偆傫丄杮摉偩丅偦傫側傆偆偵傕偱偒傞傫偩偹偉丅乿偲懳墳偟偰偟傑偭偨偺偱丄偦偺惗搆偑帺暘偺峫偊曽傪摼堄偘偵傒傫側偺慜偱敪昞偟偨丅偦偟偰丄戞俁偺夝朄偲偄偆偙偲偱傎偐偺僋儔僗偱傕徯夘偟偰偍偄偨丅
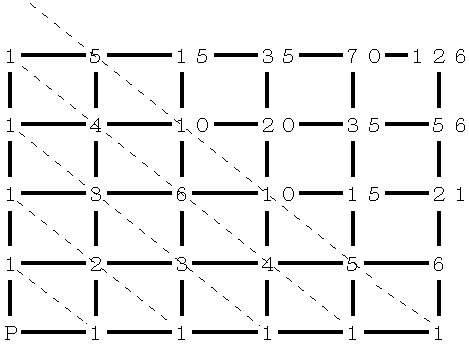
乮暿夝乯偦傟偧傟偺岎嵎揰偵擖偭偰偔傞摴弴偺憤悢傪恾偺傛偆偵彂偒崬傓偲丄侾俀俇捠傝偱偁傞丅
丂偙傟偼恾偺傛偆側妏俧偵棃傞摴弴偑丄俧偺嵍偺妏俽偍傛傃塃偺妏俿偐傜偺椉曽岦偁傝偦傟偧傟偑倠捠傝丄倣捠傝偁傞側傜偽丄俧偵棃傞摴弴偼偁傢偣偰乮倠亄倣乯捠傝偁傞偲偄偆榓偺朄懃傪梡偄偨傕偺偱偁偭偨偑丄偳傟偩偗摴偑暋嶨偱偁偭偰傕丄嵟抁宱楬偺憤悢偑媮傔傜傟傞偲偄偆偙偲偱丄惗搆偵偼寢峔岲昡偱偁偭偨丅師偺俀偮偺椺偱妋擣偟偰偍偒偨偄丅
椺侾乯
丂丂丂丂丂丂 倠捠傝仺丂 丂丂丂丂丂乮倠亄倣乯捠傝
俽 劒劒劒劒劒劒劒劒 俧
劔丂丂丂丂丂丂丂丂丂丂丂 劔
劔丂丂丂丂丂丂丂丂丂丂丂 劔仾倣捠傝
劔丂丂丂丂丂丂丂丂丂丂丂 劔
丂丂劒劒劒劒劒劒劒劒 俿
椺俀乯
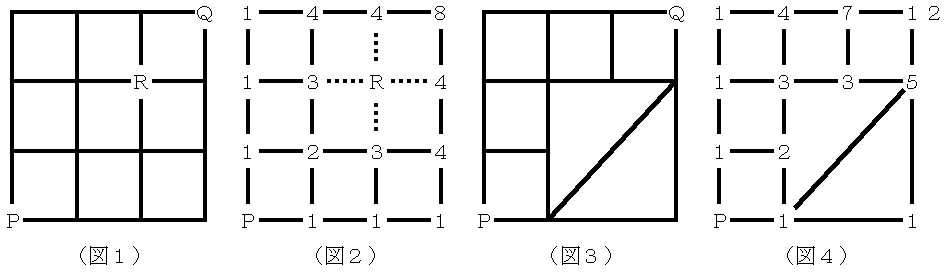
椺偊偽丄恾侾偺傛偆側宱楬偱俼傪捠傜側偄傕偺偼丄恾俀偺傛偆偵峫偊偰俉捠傝丅傑偨丄恾俁偺傛偆側宱楬偱偺嵟抁宱楬偼丄恾係偺傛偆偵峫偊偰侾俀捠傝偲丄寢峔娙扨偵媮傔傞偙偲偑偱偒傞丅
仛師偵丄偙偺撪梕傪妛廗偟偰俁偮偺僋儔僗偱摨偠偙偲傪愢柧偟偰偄偔偆偪丄愭掱偺椺戣偺悢偊忋偘偺恾傪幬傔偵傒傞偲丄僷僗僇儖偺嶰妏宍偑塀傟偰偄傞偙偲偵婥偑偮偄偨丅偦偺嶌傝曽偐傜峫偊傟偽摉慠偺偙偲偲尵偊傞偐傕偟傟側偄偑丄偙偆偟偰摴弴傪悢偊忋偘偰偄偔偙偲偵傛傝 乮倎亄倐乯値 偺揥奐帪偵偍偗傞奺崁偺學悢偑傢偐傞偺偱偁傟偽丄俁師尦傪峫偊傞偙偲偵傛偭偰丄
乮倎亄倐亄們乯値偺揥奐偑摨條偵偱偒傞偺偱偼側偄偐偲峫偊偰傒偨丅
丂
丂傑偢丄乮倎亄倐亄們乯値 偱値亖侾,俀,俁丆乧偲悢抣傪戙擖偟偰幚嵺偵揥奐傪偟偰傒傞偲丄
乮倎亄倐亄們乯侾亖倎亄倐亄們
乮倎亄倐亄們乯俀亖倎俀亄倐俀亄們俀亄2倎倐亄2倐們亄2們倎
乮倎亄倐亄們乯俁亖倎俁亄倐俁亄們俁亄3倎俀倐亄3倎俀們亄3倎倐俀亄3倐俀們亄3倎們俀亄3倐們俀亄6倎倐們
乮倎亄倐亄們乯係亖倎係亄倐係亄們係亄4倎俁倐亄4倎俁們亄4倎倐俁亄4倐俁們亄4倎們俁亄4倐們俁亄6倎俀倐俀亄12倎俀倐們亄6倎俀們俀亄12倎倐俀們亄6倐俀們俀亄12倎倐們俀
丂
偙偙傑偱揥奐偡傞偩偗偱傕崪偺偍傟傞嶌嬈偱偁偭偨丅堦曽丄棫懱儌僨儖傪嶌傝丄悢偊忋偘偺曽朄偱奺奿巕傑偱偺嵟抁宱楬悢傪彂偒崬傫偱傒偨丅偡傞偲丄摨堦暯柺忋偵偒傟偄偵揥奐偟偨偲偒偺奺崁偺學悢偑暲傫偱偄傞偙偲偑傒偰偲傟偨丅偙偺偙偲偼丄師偺儁乕僕偺恾傪傒傟偽偁偒傜偐偱偁傞丅偙偺偁偲丄値亖俆,俇丆乧 偲悢抣傪戙擖偟偰揥奐傪偟偰偄偔偙偲偑偄傛偄傛戝曄偵側偭偰偒偨偺偱丄杮峑偺撊栘嬘栫愭惗偵憡択偟偨偲偙傠丄夣偔師偺傛偆側僾儘僌儔儉傪嶌偭偰偄偨偩偔偙偲偑偱偒丄寁嶼偺庤娫傪徣偔偙偲偑偱偒偨丅偙偺僾儘僌儔儉偼丄愭掱偺悢偊忋偘偺朄懃傪偆傑偔棙梡偝傟偨傕偺偱丄棫懱儌僨儖摨條師偵嵹偣偰偍偔丅

 丂
丂